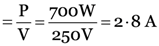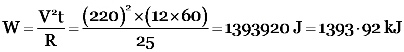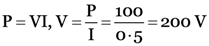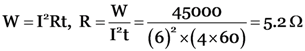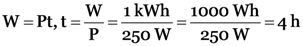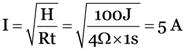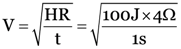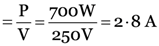Go premium Contact About Us
Logo
Home › Grade10 › Grade 10 CBSE › 10 CBSE Physics › Electricity › Worksheets on Electricity › Electricity Worksheet-11

Electricity Worksheet-11

Electricity Worksheet-11

 

  1. An electric heater draws a current of 5 A and its element has a resistance of 50 Ω. If the heater is switched on for 5 minutes, calculate the energy released in kilojoules.

 

  1. An electric room heater has a resistance of 25 Ω and operates at 220 V for 12 minutes. Calculate heat energy dissipated by it in kilojoules.

 

  1. Calculate the total power of 5 fans if each of them draws a current of 0.8 A at a potential difference of 220 V.

 

  1. An electric bulb of resistance 400 Ω, draws a current of 0.5 A. Calculate the power of the bulb and the potential difference at its ends.

 

  1. A soldering rod iron draws an energy of 45000 J in 4 minutes when the current flowing through its element is 6 A. Calculate the resistance of its heating element.

 

  1. An electric bulb is marked 250 W-200 V. what information does it convey? How many joules of energy is consumed by this bulb in one hour? How long will it take for the bulb to consume 1 k Wh?

 

  1. 100 J of heat are produced each second in a 4 Ω resistance. Find the potential difference across the resistor.

 

  1. An electric bulb is connected to a 220 V generator. The current is 0.50 A. What is the power of the bulb?

 

  1. An electric refrigerator rated 400 W operates 8 hour/day. What is the cost of the energy to operate it for 30 days at Rs. 3.00 per kWh?

 

  1. Two bulbs 0f 100 W each and two coolers of 250 W each, work on an average 6 hours a day. If the energy costs Rs. 1.75 per kWh, calculate the monthly bill and the minimum fuse rating when power is supplied at 250 V.

 

Answer:

  1. W = I2Rt = (5)2 × (50) × (5 × 60) = 375000 J = 375 kJ

 

 

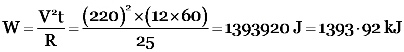
  1. P = VI = 220 × 0.8 = 176 W. Power of 5 fans = 5 × 176 = 880 W

 

  1. P = I2R = (0.5)2 × 400 = 100 W

As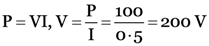    

 

 

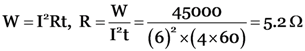
  1. A 250 W – 200 V bulb consumes an electric power of 250 W when working on 200 V and the resistance of such a bulb is (200)2/250 = 160 Ω (as P = V2/R or R = V2/P)

W = Pt = 250 × (60 × 60) = 900000 J

As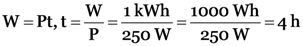

 

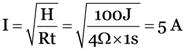
V = IR = 5 A × 4 Ω = 20 V

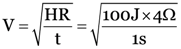
= 20 V

 

  1. P = VI = 220 V × 0.50 = 110 W

 

  1. Total energy consumed in 30 days, i.e., W = Pt = 400 W × 8 hour/day × 3 days = 96000 Wh = 96 kWh.

Cost of energy = 96 kWh × Rs.3.00 kWh = Rs. 2880.00

 

  1. Total power, P = 2 × 100 + 2 × 250 = 700 W

Electric energy consumed per month

= P × t = (700 W) (6 h) (30)

= 126000 Wh = 126 kWh (1 month = 30 days)

Monthly bill = 126 × 1.75 = Rs. 220.50

As P = VI, I (minimum fuse rating)