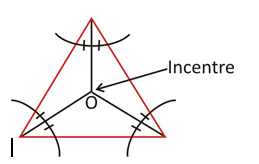
Incentre is concurrence point of angle bisectors of triangle. The three sides of the triangle are tangents to the cirle with centre O.
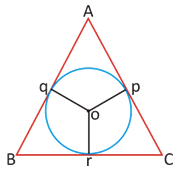
Radius of in circle of an equilateral triangle of side a = a/2Ö3
op = oq = or = radius or Inradius and o is incentre
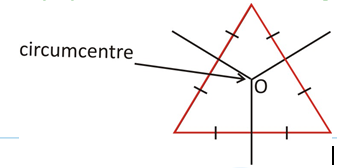
· Circum centre is concurrence point of perpendicular bisectors of a triangle.
Radius of circum circle of an equilateral triangle of side a = a/Ö3
OP = OQ = OR Þ Circum Radius O is circum centre
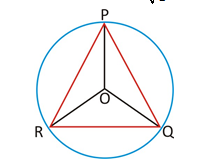
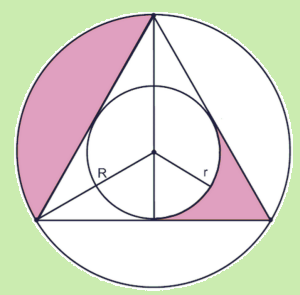
· Relationship between inradius and circumradius:
If r is radius of incircle & R is radius of circumcircle then
A (area of triangle) = pr = abc/4R
where a, b & c are sides of the triangle and p is semi perimeter of the triangle.
p = ( a+b+c)/2
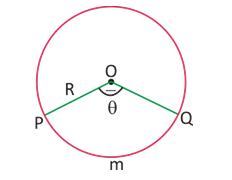
Area of circle = ÕR2, where R is the radius of the circle. OP = R = Radius
Circumference of a circle = 2ÕR. This is also known as perimeter of circle.
Length of arc, is 2ÕR q/360 where q is the central angle.
Are of a sector = Area of sector POQ = ÕR2q/360
Area of a semi-circle ÕR2/2.
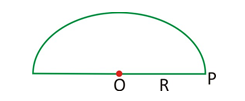
Circumference of a semi-circle = ÕR.
Perimeter of a semicircle is ÕR + 2R