Electricity Worksheet-6
Answer:
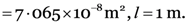
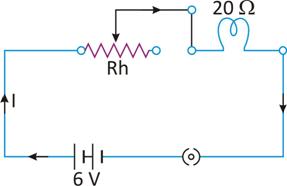
As 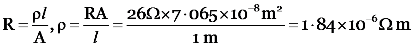
Resistance of the lamp, r = 20 Ω
Current in the circuit, I = 0.25 A
Let R1 be the resistance required from the variable resistance to be placed in series with the lamp.
Total resistance in the circuit, R = R1 + r = R1 + 20
Ohm’s law 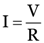
Or 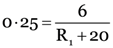
or 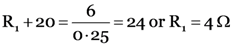
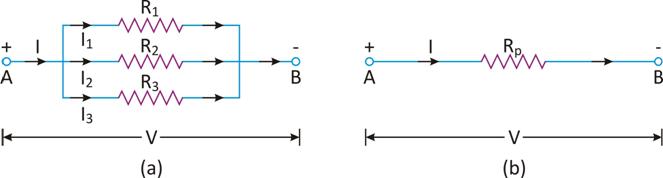
Thus, I1 (current through R1) 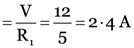
I2 (current through R2) 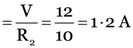
I3 (current through R3) 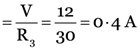
(b) total current in the circuit,
I = I1 + I2 + I3 = 2.4 + 1.2 + 0.4 A
(c) If RP is the total resistance in the circuit, then
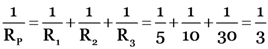
or Rp = 3 Ω
we can also find the total current by first calculating RP and then using,
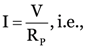
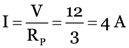
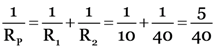
Or 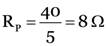
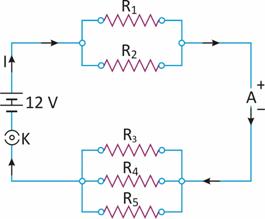
Further, as R3, R4 and R5 are in parallel, their resultant resistance (RP) is given by
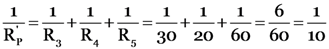
RP = 10 Ω
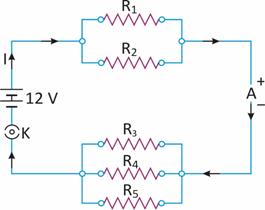
As RP and Rp are in series, total resistance in the circuit,
Rs = Rp + Rp = 8 + 10 = 18 Ω
Total current in the circuit, i.e., 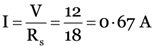
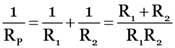
Or 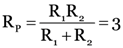 …(i)
…(i)
When R1 and R2 are connected in series, net resistance (Rs) given by
Rs = R1 + R2 = 16 ….(ii)
From (i) and (ii), 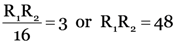
Or R1(16 – R1) = 48
(as R1 + R2 = 16, R2 = 16 – R1)
Or 26R1 – R12 = 48
Or R12 – 16R1 + 48 = 0
Or (R1 – 12) (R1 – 4) = 0
Thus, either R1 = 12 Ω or 4 Ω
R2 = 4 Ω or 12 Ω
Therefore, the resistances of two resistors are 4 Ω and 12 Ω.