Gravitation Worksheet-2

Gravitation Worksheet-2

Calculate the force of gravitation due to earth on a ball of 1 kg mass lying on the ground. (Mass of earth = 6 × 10²⁴ kg; Radius of earth = 6.4 × 10³ km; and G = 6.7 × 10^–11 Nm²/Kg²)

A. 9.8 newtons B. 10 newtons

C. 9.8 kg D. 9.8 newton meter

The mass of the earth is 6.4 × 10²⁴ kg and that of the moon is 7.4 × 10²² kg. if the distance between the earth and the moon be 3.84 × 10⁵ km, calculate the force exerted by the earth on the moon. (G = 6.7 × 10^–11 Nm² kg^–2)

A. F = 2.01 × 10¹⁰ newtons

B. F = 2.01 × 10²⁰ kg

C. F = 2.01 × 19²⁰ newton meter

D. F = 2.01 × 10²⁰ newtons

Calculate the value of acceleration due to gravity on the surface of the moon. (Given Mass of the moon = 7.4 × 10²² kg; Radius of moon = 1740 km; G = 6.67 × 10^–11 Nm² /kg²)

A. –1.63 m/s² B. 1.63 m/s C. 1.63 m/s² D. 9.8 m/s²

The earth’s gravitational force causes an acceleration of 5 m/s² in a 1 kg mass somewhere in space. How much will the acceleration of a 3 kg mass be at the same place ?

A. 5 m/s² B. -5 m/s² C. 15 m/s² D. 5/3 m/s²

To estimate the height of a bridge over a river, a stone is dropped freely in the river from the bridge. The stone takes 2 seconds to touch the water surface in the river. Calculate the height of the bridge from the water level (g = 9.8 m/s²)

A. 39.2 m B. 20 m C. 9.8 m D. 19.6 m

Answer Key:

Explanation: The force of gravitation is calculation is calculated by using the formula:

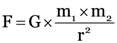
Gravitational constant, G = 6.7 × 10^–11 Nm²/Kg²

Mass of earth, m₁ = 6 × 10²⁴ kg

Mass of ball, m₂ = 1 kg

Distance between centre of earth and ball

r = Radius of earth

= 6.4 × 10³ km

= 6.4 × 10³ × 1000m

= 6.4 × 10⁶ km

By putting these values in the formula, we get :

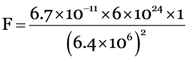
Or F = 9.8 newtons

Thus, the earth exerts a gravitational force of 9.8 newtons on a ball of mass 1 kilogram. This is a comparatively large force. It is due to this large gravitational force exerted by earth that when the 1 kg ball is dropped from a height, it falls to the earth.

Explanation: The force exerted by one body on another body is given by the newton’s formula:

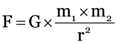
Here, Gravitational constant, G = 6.7 × 10^–11 Nm² kg^–2

Mass of the earth, m₁ = 6 × 10²⁴ kg

Mass of the moon, m₂ = 7.4 × 10²² kg

Distance between Earth and moon

r = 3.84 × 10⁵ km

= 3.84 × 10⁸ km

By putting the values in the formula, we get :

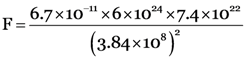
F = 2.01 × 10²⁰ newtons

Thus, the gravitational force exerted by the earth on the moon is 2.01 × 10²⁰ newtons. And this is an extremely large force. It is this extremely large gravitational force exerted by the earth on the moon which makes the moon revolve around the earth.

Explanation: The formula for calculating the acceleration due to gravity is :

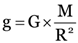
Gravitational constant, G = 6.7 × 10^–11 Nm²/kg²

Mass of the moon, M = 7.4 × 10²² kg

Radius of the moon, R = 1740 km

1.74 × 10⁶ m

Now, putting these values in the formula, we get :

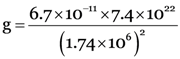
Or g = 1.63 m/s²

Thus, the acceleration due to gravity, g, on the surface of the moon is 1.63 m/s².

Explanation: The acceleration produced by the gravitational force of earth does not depend on the mass of the object. So, the acceleration produced in the 3 kg mass will be the same as that produced in 1 kg mass. That is, the acceleration produced will be 5 m/s².

Explanation: The stone is dropped freely from rest, so the initial velocity of the stone, u = 0. Again, the velocity of stone is increasing as it comes down, so the acceleration due to gravity, g, is positive.

Now, initial velocity of stone, u = 0

Time taken, t = 2 s

Acceleration due to gravity, g = 9.8 m/s² (stone is coming down)

And, Height of the bridge, h = ?

For a freely falling body :

Height, h = ut + (1/2) gt²

Putting the values in the formula, we get :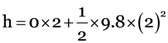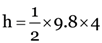

Or h = 19.6 m

Thus, the height of bridge above the water level is 19.6 metres.