Light reflection and refraction Worksheet-1

Light reflection and refraction Worksheet-1

1. Fine the focal length of a convex mirror of radius of curvature 1 m.

A. 0.5 m                                          B. 1 m

C. 0.25 m                                       D. None of these

2. An object 4 cm in size is placed at a distance of 25.0 cm from a concave mirror of focal length 15.0 cm. find the position nature and height of the image.

A. –37.5 cm, real and inverted, –6 cm

B. –37.5 cm, virtual and inverted, –1.5 cm

C. 37.5 cm, real and erect, –6 cm

D. None of these

3. A converging mirror forms a real image of height 4 cm, of an object of height 1 cm placed 20 cm away from the mirror. Calculate the image distance. Find the focal length of the mirror ?

A. 16 cm             B. –16 cm          C. 20 cm            D. –20 cm

4. A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and magnification.

A. 6.7 cm behind the mirror and m = 0.7

B. 6.7 cm behind the mirror and m = 0.558

C. 6.7 cm in front of  the mirror and m = 0.558

D. None of these

5. An arrow 2.5 cm high is placed at a distance of 25 cm from a diverging mirror of focal length 20 cm. find the size of the image formed.

A. 1.1 cm                                         B. 2.5 cm

C. 2.2 cm                                        D. None of these

Answer Key:

1. A

focal length f = ?

Radius of curvature, R = 1 m (+ for convex mirror)

As     f = R/2

∴     f = 1/2m = 0.5 m

2. A

Height of the object, h₁ = +4 cm

Object distance, u = –25.0 cm

Focal length of concave mirror, f = –15.0 cm

(i) position of image. Using mirror formula :

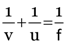
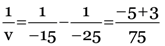
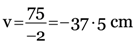
          i.e. image distance v = –37.5 cm

Thus, position of image is 37.5 cm in front of the mirror, because v is negative.

(ii) Nature of image. Since the image is formed in front in front of the mirror, it must be real and inverted.

(iii) Height of image. Using the expression for linear magnification, 

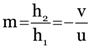
Here h₁ = +4 cm, u = –25.0 cm and v = –37.5 cm

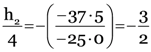
          h₂ = –6cm

Therefore, height of image is 6 cm. the minus sign shows that the image is below the principal axis. Therefore, it is inverted and real.

3. B

Height of image, h₂ = –4 cm, minus sign is for real image, which is inverted or we can say below the principal axis.

Height of object, h₂ = +1 cm

Object distance u = –20 cm; minus sing for object distance is measured from pole in a direction opposite to the direction of incidence of light.

We have to calculate the image distance, u = ?

As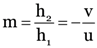

∴ putting the values in the formula we get 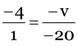or v = –80 cm

Negative sign of v indicates that the image is on the side of the object. It must be real and inverted.

To calculate focal length of the mirror, we use mirror formula: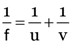

Putting u = –20 cm and v = –80 cm.

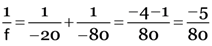
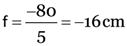
Negative sign of f indicates that mirror is concave.

4. B

Object size h₁ = 4.5 cm

Object distance u = –12 cm

Focal length, f = +15 cm

Image distance, v = ?

Magnification m = ?

As Mirror formula :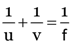

                   ∴

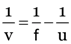
putting u = –12 cm and f = +15 cm. we get

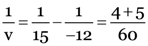
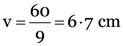
i.e., image is formed 6.7 cm behind the convex mirror. It must be virtual and erect.

If h₂ is size of the image, then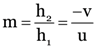

or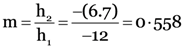     

i.e., h₂ = 0.558 h₁ = 0.558 × 4.5 = 2.5 cm

As the needle is moved farther from the mirror, image moves away from the mirror till it is at focus F of the mirror. The size of the image goes on decreasing.

5. A

Object size, h₁ = +2.5 cm

          Object distance, u = –25 cm

          Focal length of diverging mirror, f = +20 cm

          Image distance, v = ?

Using mirror formula,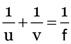   

or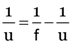   

And putting the values u = –25 cm and f = +20 cm, we get

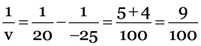
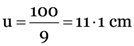
Since image is at the back of the mirror at 11.1 cm from the mirror, it must be virtual and erect. It h₂ is the size of the image, then

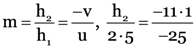
or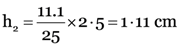     

This is the size of the image.