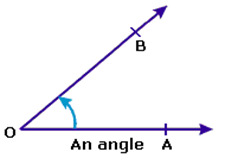
Angles: When two straight lines meet at a point they form an angle. In the figure, the angle is represented as ∠AOB. OA and OB are the arms of ∠AOB. Point O is the vertex of ∠AOB. The amount of turning from one arm (OA) to other (OB) is called the measure of the angle (AOB).
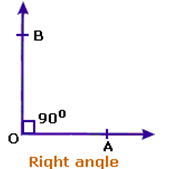
Right angle: An angle whose measure is 90° is called a right angle. ∠BOA is a right angle in the figure.
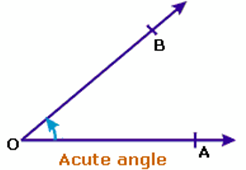
Acute angle: An angle whose measure is less then one right angle (i.e., less than 90°), is called an acute angle.
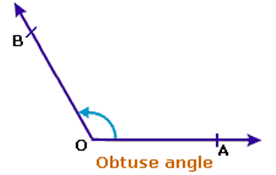
Obtuse angle: An angle whose measure is more than one right angle i. e. 90° and less than two right angles
(i.e., less than 180° and more than 90°) is called an obtuse angle.
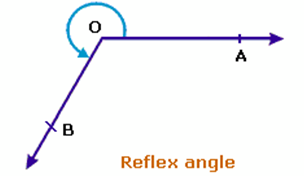
Reflex angle: An angle whose measure is more than 180° and less than 360° is called a reflex angle.
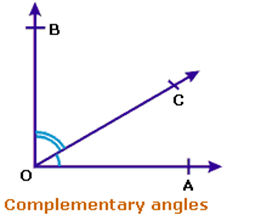
Complementary angles: If the sum of the two angles is one right angle (i.e., 90°), they are called complementary angles. Therefore, the complement of an angle θ is equal to 90° − θ. ∠AOC & ∠COB are Complementary angles.
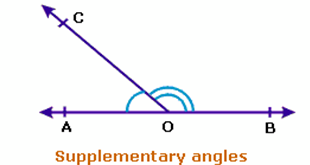
Supplementary angles: Two angles are said to be supplementary, if the sum of their measures is 180°. Here ∠BOC & ∠COA are Supplementary angles.
Example:
Angles measuring 130o and 50o are supplementary angles. Two supplementary angles are the supplement of each other. Therefore, the supplement of an angle θ is equal to 180° − θ.
The sum of all the angles round a point is equal to 360°.
If two lines intersect, then the vertically opposite angles are equal.
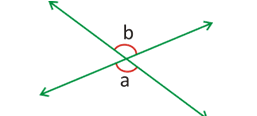
Angle a = angle b (vertically opposite angle)
If a transversal intersects two parallel lines, then each pair of corresponding angles are equal.
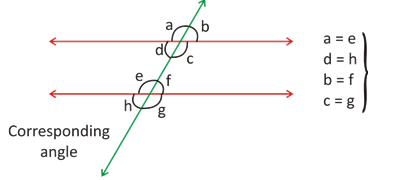
Other facts :
a + b = 180°
a = c & b = d e = g & f = h
c = e, d = f
c + f = d + e = 180°
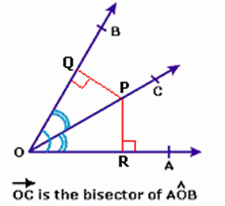
Bisector of an angle: If a ray or a straight line passing through the vertex of that angle, divides the angle into two angles of equal measurement, then that line is known as the Bisector of that angle.
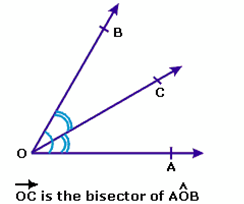
A point on an angle is equidistant from both the arms.
In the figure, Q and R are the feet of perpendiculars drawn from P to OB and OA. It follows that
PQ = PR.