Permutations
Introduction:
► The Factorial:
n! = n (n – 1) (n – 2) ......3.2.1.
► we define 0! = 1.
► when n is negative or a fraction, n! is not defined
Exponent of Prime p in n!:
► Let p be a prime number and n be a positive integer. Then the last integer amongst 1, 2, 3,..... (n – 1), n which is divisible by p is [n/p]p, where [n/p] denotes the greatest integer less than or equal to n/p.
Number of Permutations without Repetition:
► Arranging n objects, taken r at a time equivalent to filling r places from n things.
nPr = n!/(n–r)!
► The number of arrangements of n different objects taken all at a time = nPn = n!
(i) nP0 = (n!/n!) = 1; nPr = n.n–1Pr–1.
(ii) 0! = 1; (1/(–r)!) = 0 or (–r)! = ∞ (r ∊ N)
Number of Permutations with Repetition:
► The number of permutations = The number of ways of filling r places = (n)4.
► The number of arrangements that can be formed using n objects out of which p are identical (and of one kind) q are identical (and of another kind), r are identical (and of another kind) and the rest are distinct is n!/(p!q!r!).
Conditional Permutations:
► Number of permutations of n dissimilar things taken r at a time when p particular things always occur = nPr.
► Number of permutations of n dissimilar things taken r at a time when p particular things never occur = n–PCrr!.
► The total number of permutations of n different things taken not more than r at a time, when each thing may be repeated any number of times, is (n(nr – 1))/(n–1).
► Number of permutations of n different things, taken all at a time, when m specified things always come together is m! × (n – m + 1)!.
► Number of permutations of n different things, taken all at a time, when m specified things never come together is n! – m! × (n – m + 1)!.
► Let there be n objects, of which p1 are alike of one kind; p2 are alike of another kind; p3 are alike of 3rd kind;......; pr are alike of rth kind such that p1 + p2 + ... + pr = n; then the number of permutations of these n objects is n!/ (p1!) × (p2!) × ... × (pr!).
Circular Permutations:
► In circular permutations, what really matters is the position of an object relative to the others.
► There are two types of circular permutations:
► The circular permutations in which clockwise and the anticlockwise arrangements give rise to different permutations, e.g. seating arrangements of persons round a table.
► The circular permutations in which clockwise and the anticlockwise arrangements give rise to same permutations, e.g. arranging some beads to form a necklace.
Difference between Clockwise and Anti-clockwise Arrangement:
► If anti-clockwise and clockwise order of arrangement are not distinct e.g., arrangement of beads in a necklace, arrangement of flowers in garland etc. then the number of circular permutations of n distinct items is (n – 1)!/ 2.
► Number of circular permutations of n different things, taken r at a time, when clockwise and anticlockwise orders are taken as different is nPr/r.
► Number of circular permutations of n different things, taken r at a time, when clockwise and anticlockwise orders are not different is nPr/2r.
Theorems on Circular Permutations
Theorem (i): The number of circular permutations of n different objects is (n – 1)!.
Theorem (ii): The number of ways in which n persons can be seated round a table is (n – 1)!.
Theorem (iii): The number of ways in which n different beads can be arranged to form a necklace, is (1/2) (n–1)!.
Combinations
► The number of all combinations of n things, taken r at a time is denoted by C(n,r) or nCr or (n r).
► nCr is always a natural number.
Number of Combinations without Repetition:
► The number of combinations (selections or groups) that can be formed from n different objects taken r(0 ≤ r ≤ n) at a time is nCr = n! (r!(n – r)!). Also nCr = nCn–r.
Number of Combinations with Repetition and all Possible Selections:
► The number of combinations of n distinct objects taken r at a time when any object may be repeated any number of times.
= Coefficient of x' in (1 + x + x2 + ... + xr)n
= Coefficient of x' in (1 – x)–n = n+r–1 Cr
► The total number of ways in which it is possible to form groups by taking some or all of n things at a time is nC1 + nC2 + ... + nCn = 2n – 1.
► The total number of ways in which it is possible to make groups by taking some or all out of n = (n1 + n2 + ...) things, when n1 are alike of one kind, n2 are alike of second kind, and so on is {(n1 + 1) (n2 + 1) ...} –1.
► The number of selections of r objects out of n identical objects is 1.
► Total number of selections of zero or more objects from n identical objects is n + 1.
► The number of selections taking at least one out of a1 + a2 + a3 + + ... + an + k objects, where a1 are alike (of one kind), a2 are alike (of second kind) and so on ...... an are alike (of nth kind) and k are distinct = [(a1 + 1) (a2 + 1) (a3 + 1) ... (an + 1)]2k – 1.
Conditional Combinations
► The number of ways in which r objects can be selected from n different objects if k particular objects are
(i) Always included = n–kCr–k
(ii) Never included = n–kCr
► The number of combinations of n objects, of which p are identical, taken r at a time is
n–pCr + n–pCr–1 + n–pCr–2 + ... + n–pC0, if r ≤ p and
n–pCr + n–pCr–1 + n–pCr–2 + ... + n–pCr–p, if r > p
Division into Groups
Case I:
► The number of ways in which n different things can be arranged into r different groups is n+r–1Pn or n ! n–1Cr–1 according as blank group are or are not admissible.
► The number of ways in which n different things can be distributed into r different group is rn – rC1(r – 1)n + rC2(r – 2)n – ... + (–1)n–1 nCr–1 or Coefficient of xn is n ! (ex – 1)r.
► Here blank groups are not allowed.
► Number of ways in which m × n different objects can be distributed equally among n persons (or numbered groups) = (number of ways of dividing into groups) × (number of groups)! = ((mn)!n!)/(m!)nn! = (mn)!/(m!)n.
Case II:
► The number of ways in which (m + n) different things can be divided into two groups which contain m and n things respectively is, m+nCm. nCn = (m+n)!/m!n!, m ≠ n.
Corollary: If m = n, then the groups are equal size. Division of these groups can be given by two types.
Type I: If order of group is not important: The number of ways in which 2n different things can be divided equally into two groups is (2n)!/(2!(n!)2).
Type II: If order of group is important : The number of ways in which 2n different things can be divided equally into two distinct groups is (2n)!/(2!(n!)2) × 2! = 2n!/(n!)2.
► The number of ways in which (m + n + p) different things can be divided into three groups which contain m, n and p things respectively is m+n+pCm.n+pCn.pCp = (m+n+p)!/(m!n!p!), m ≠ n ≠ p.
Corollary: If m = n = p, then the groups are equal size. Division of these groups can be given by two types.
Type I: If order of group is not important: The number of ways in which 3p different things can be divided equally into three groups is (3p)!/(3!(p!)3).
Type II: If order of group is important: The number of ways in which 3p different things can be divided equally into three distinct groups is ((3p)!/(3!(p!)3))3! = (3p)! = (p!)3.
(i) If order of group is not important: The number of ways in which mn different things can be divided equally into m groups is mn!/((n!)m m!)
(ii) If order of group is important: The number of ways in which mn different things can be divided equally into m distinct groups is (mn)!/(n!)mm! × m! = (mn)!/(n!)m.
Derangement
► Any change in the given order of the things is called a derangement.
► If n things form an arrangement in a row, the number of ways in which they can be deranged so that no one of them occupies its original place is 
.
► Number of total different straight lines formed by joining the n points on a plane of which m (< n) are collinear is nC2 – mC2 + 1.
► Number of total triangles formed by joining the n points on a plane of which m (< n) are collinear is nC3 – mC3.
► Number of diagonals in a polygon of n sides is nC2 – n.
► If m parallel lines in a plane are intersected by a family of other n parallel lines. Then total number of parallelograms so formed is nC2 × nC2 i.e., (mn(m – 1) (n – 1))/4.
► Given n points on the circumference of a circle, then
(i) Number of straight lines = nC2
(ii) Number of triangles = nC3
(iii) Number of quadrilaterals = nC4.
► If n straight lines are drawn in the plane such that no two lines are parallel and no three lines are concurrent. Then the number of part into which these lines divide the plane is = 1 + ∑n.
► Number of rectangles of any size in a square of n × n is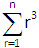 
and number of squares of any size is .jpg)
.
► In a rectangle of n × p(n < p) number of rectangles of any size is ((np)/4) (n + 1) (p + 1) and number of squares of any size is .jpg){kind=small}
.
► Let x1, x2 , ... xm be integers. Then number of solutions to the equation
x1 + x2 + ... xm = n .... (i)
► Subject to the condition
a1≤x1≤b1, a2≤x2≤b2, ... am≤xm≤bm ..... (ii)
is equal to the coefficient of xn in
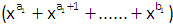
.jpg)
.jpg)
..... (iii)
This is because the number of ways, in which sum of m integers in (i) equals n, is the same as the number of times xn comes in (iii).
► Use of solution of linear equation and coefficient of a power in expansions to find the number of ways of distribution: The number of integral solutions of x1 + x2 + x3 + ... + xr = n where x1 ≥ 0, x2 ≥ 0, ... x2 ≥ 0, ... xr ≥ 0 is the same as the number of ways to distribute n identical things among r persons.
This is also equal to the coefficient of xn in the expansion of (x0 + x1 + x2 + x3 + ...)r 
.
► The number of integral solutions of x1 + x2 + x3 + ... xr = n ... + xr = n where x1 ≥ 1, x2 ≥ 1, ... xr ≥ 1 is same as the number of ways to distribute n identical things among r persons each getting at least 1. This also equal to the coefficient of xn in the expansion of (x1 + x2 + x3 + ...)r.
.
► Let 
, where p1, p2, p3, ... pk are different primes and α1, α2, α3, ... αk are natural numbers then:
► The total number of divisors of N including 1 and N is = (α1 + 1) (α2 + 1) (α3 + 1) ... (αk + 1)
► The total number of divisors of N excluding 1 and N is = (α1 + 1) (α2 + 1) (α3 + 1) ... (αk + 1) – 2
► The total number of divisors of N excluding 1 or N is = (α1 + 1) (α2 + 1) (α3 + 1) ... (αk + 1) – 1.
► The sum of these divisors is
.jpg){kind=small}
.jpg)
► The number of ways in which N can be resolved as a product of two factors is
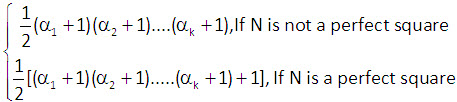
► The number of ways in which a composite number N can be resolved into two factors which are relatively prime (or co-prime) to each other is equal to 2n–1 where n is the number of different factors in
Points at the Glance
► nC0 = nCn = 1, nC1 = n.
► nC4 + nCr–1 = n+1Cr.
► nCx = nCy ⇔ x = y or x + y = n.
► n. n–1Cr–1 = (n – r + 1) nCr–1.
► If n is even then the greatest value of nCr is nCn/2.
► If n is odd then the greatest value of nCr is nC(n+1)/2 or nC(n–1)/2. nCr = n/r. n–1Cr–1
► Number of selections of zero or more things out of n different things is, nC0 + nC1 + nC2 + ... + nCn = 2n.
► The number of ways of answering one or more questions when each question has an alternative is, 3n – 1.
► The number of ways of answering all of n questions when each question has an alternative is 2n.
► nC0 + nC2 + nC4 + ... = nC1 + nC3 + nC5 + ... = 2n–1.
► 2n+1C0 + 2n+1C1 + 2n+1C2 + ... + 2n+1Cn = 22n.
► nCn + n+1Cn + n+2Cn + n+3Cn + ... + 2n–1Cn = 2nCn+1.
► Number of combinations of n dissimilar things taken all at a time
► The number of ways in which n (one type of different) things and n (another type of different) things can be arranged in a row alternatively is 2.n!.n!..
► The number of ways in which m things of one type and n things of another type can be arranged in the form of a garland so that all the second type of things come together = (m!n!)/2 and no two things of second type come together = ((m – 1)! mPn)/2.
► All the numbers whose last digit is an even number 0, 2, 4, 6 or 8 are divisible by 2.
► All the numbers sum of whose digits are divisible by 3, is divisible by 3. e.g., 534. Sum of the digits is 12, which are divisible by 3, and hence 534 is also divisible by 3.
► All those numbers whose last two-digit number is divisible by 4 are divisible by 4. e.g., 7312, 8936, are such that 12, 36 are divisible by 4 and hence the given numbers are also divisible by 4.
► All those numbers, which have either 0 or 5 as the last digit, are divisible by 5.
► All those numbers, which are divisible by 2 and 3 simultaneously, are divisible by 6. e.g., 108, 756 etc.
► All those numbers whose last three-digit number is divisible by 8 are divisible by 8.
► All those numbers sum of whose digit is divisible by 9 are divisible by 9.
► All those numbers whose last two digits are divisible by 25 are divisible by 25. e.g., 73125, 2400 etc.
