► Angles opposite to two equal sides of a triangle are equal.
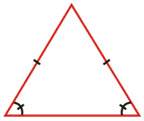
► If two angles of a triangle are equal, then the sides opposite to them are also equal.
► If two sides of a triangle are unequal, the longer side has greater angle opposite to it.
► A triangle is isosceles if and only if any two altitudes are equal.
► If the bisector of the vertical angle of a triangle bisects the base then the triangle is isosceles.
► The medians of an equilateral triangle are equal.
Midpoint Theorem:
► The line segment joining the midpoints of two sides of a triangle is parallel to the third side and equal to half of it.
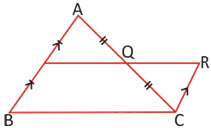
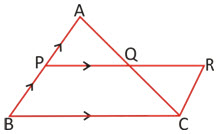
Converse of Theorem:
► The straight line drawn through the midpoint of one side of a triangle parallel to another side, bisects the third side.
Pythagoras Theorem:
Theorem 1:
► In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Hence, BC2 = CA2 + AB2
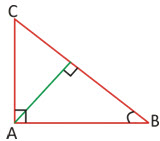
Theorem 2:
► In a triangle, if the square on one side is equal to the sum of the squares on the remaining two sides, the angle opposite to the first side is a right angle.
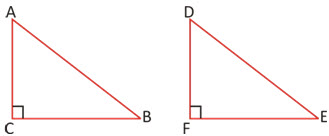
Pythagorean Triplets:
► The three nos. that satisfy Pythagoras theorem are Pythagorean triplets.
Let the three sides be AB, AC, BC.
AC2 + AB2 = BC2
32 + 42 = 52
52 + 122 = 132
82 + 152 = 172
72 + 242= 252
(3, 4, 5), (5, 12, 13)
(8, 15, 17), (7, 24, 25)
are Pythagorean triplets.
If a, b, c are Pythagorean triplets then ax, bx, cx will also be Pythagorean triplets.
Proof:
a2 + b2 = c2
multiplying by x2 both the sides
a2x2 + b2x2 = c2x2
(ax)2 + (bx)2 = (cx)2
i.e., (ax, bx, cx) are Pythagorean triplets.
Similar Triangles:
ΔABC and ΔDEF are said to be similar, if their corresponding angles are equal and the corresponding sides are proportional.
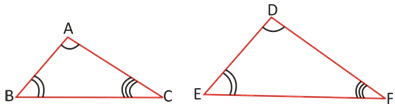
i.e., when ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
and (AB/DE) = (BC/EF) = (AC/DF)
And, ΔABC ~ ΔDEF
The sign ‘~’ is read as ‘is similar to’.
Three Similarity Axioms for Triangles:
SAS-Axiom: If two triangles have a pair of corresponding angles equal and the sides including them proportional, then the triangles are similar.
AA-Axiom or AAA-Axiom: If two triangles have two pairs of corresponding angles equal, the triangles are similar.
SSS-Axiom: If two triangles have their three pairs of corresponding sides proportional, then the triangles are similar.
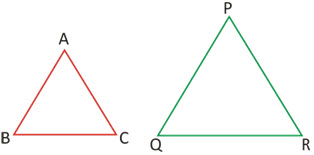
Different Results when ΔBC ~ ΔPQR
(AB/PQ) = (BC/QR) = (AC/PR)
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R
![]()
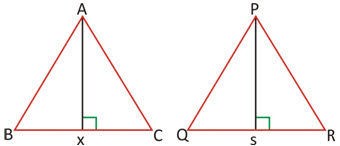
Ax & Ps are altitudes
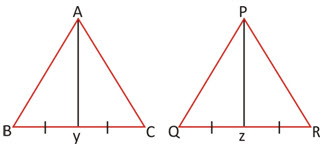
Ay & Pz are medians
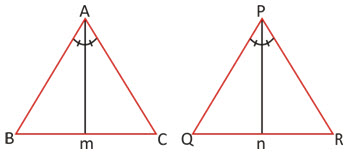
Am & Pn are angle bisectors.
![]()
Congruent Triangles:
ΔABC ≅ ΔPQR
► Two triangles are congruent if and only if their corresponding sides and the corresponding angles are equal.
► Two triangles are congruent if two sides and the included angle of one are equal to the corresponding sides and the included angle of other triangle. (SAS Congruence)
► Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle. (ASA Congruence)
► If any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle respectively, then the two triangles are congruent.
► Two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle. (SSS Congruence)
► Two right triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of the other triangle. (RHS Congruence)