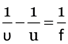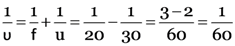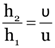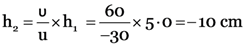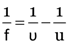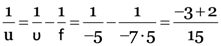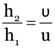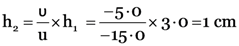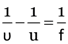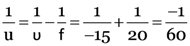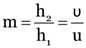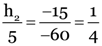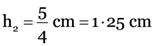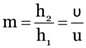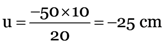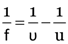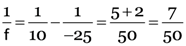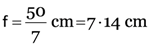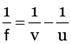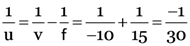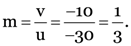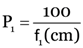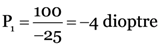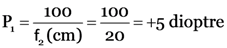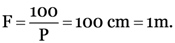Light reflection and refraction Worksheet-21
-
A convex lens has focal length of 30 cm. Calculate at what distance should the object be placed from the lens so that it forms an image at 60 cm on the other side of the lens ? Find the magnification produced by the lens in this case.
-
Find the position, nature and size of the image of an object 3 cm high placed at a distance of 9 cm from a concave mirror of focal length 18 cm.
-
An object 4 cm high is placed 40.0 cm in front of a concave mirror of focal length 20 cm. Find the distance from the mirror, at which a screen be placed in order to obtain a sharp image. Also, find the size and nature of the image formed.
-
An object is placed at a distance of 12 cm in front of a concave mirror. It forms a real image four times larger than the object. Calculate the distance of the image from the mirror.
-
A 5.0 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 20 cm. The distance of the object from the lens is 30 cm. By calculation, determine (i) the position (ii) the size of the image formed.
-
An object 30 cm high is placed perpendicular to the principal axis of a concave lens of focal length 7.5 cm. The image is formed at a distance of 5.0 cm from the lens. Calculate (i) distance at which object is placed, and (ii) size and nature of image formed.
-
A concave lens has focal length of 20 cm. At what distance from the lens a 5 cm tan object be placed so that it forms an image at 15 cm from the lens? Also, calculate the size of the image formed.
-
An object 50 cm tall is placed on the principal axis of a convex lens. Its 20 cm tall image is formed on the screen placed at a distance of 10 cm from the lens. Calculate the focal length of the lens.
-
A concave lens has focal length of 15 cm. At what distance should an object from the lens be placed so that it forms an image at 10 cm from the lens? Also, find the magnification of the lens.
-
A concave lens of focal length 25 cm and a convex lens of focal length 20 cm are placed in contact with each other. What is the power of this combination? Also, calculate focal length of the combination.
Answer:
-
Here, f = 30cm, u = ?, v = 60cm, m = ?
As 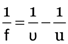
∴ 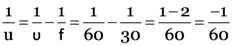
u = –60 cm
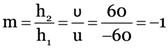
Negative sign of m indicates that image is inverted.
-
Here, the image position/distance, v = 1
Image size, h2 = ?
object size, h1 = 3 cm
object distance, u = –9 cm
Focal length of concave mirror, f = –18 cm
As 
∴ 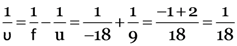
v = 18 cm
Positive sign of v shows that the image is virtual.
Again, 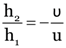
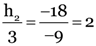
h2 = 6 cm
Positive sign of h2 shows that the image is erect and it is magnified.
-
Here, h1 = 4 cm, u = –40 cm, f = –20cm, v = ?, h2 = ?
From 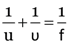
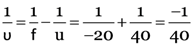
v = –40 cm
Screen should be kept at 40 cm from the mirror.
From 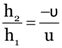
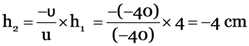
The image is real, inverted and of size = 4 cm.
-
Here, u = –12 cm, m = –4, v = ?
As 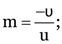
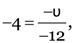 v = –48 cm.
v = –48 cm.
-
Here, h1 = 5.0 cm, f = 20cm
u = –30 cm, v = ?, h2 = ?,
From 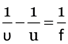
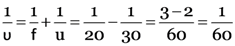
v = –60 cm
∴ Image is formed on the other side of the lens at 60 cm from the lens.
From 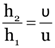
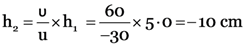
Negative sign shows that image is inverted and real. Its size is 10 cm.
-
Here, h1 = 3.0 cm, f = –7.5 cm, v = –5.0 cm
u = ?, h2 = ?
From 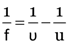
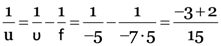
i.e., object is at 15 cm from the concave lens.
From 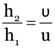
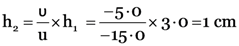
The image is virtual and erect and its size is 1 cm.
-
Here, f = –20 cm
u = ?, h1 = 5 cm
v = –15 cm, h2 = ?
As 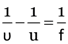
∴ 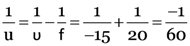
u = –60 cm
From 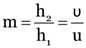
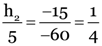
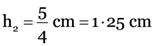
This is the height of virtual image.
-
Here, h1 = 50 cm, h2 = –20 cm
v = 10 cm, f = ?
As image is formed on the screen, it must be real and inverted. That is why h2 is negative.
From 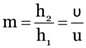
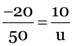
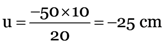
Using lens formula
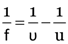
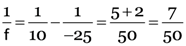
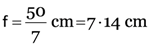
-
Here, focal length of concave lens, f = –15 cm
Object distance, u = ?
Image distance, v = –10 cm
Magnification of lens, m = ?
As 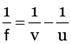
∴ 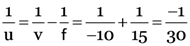
0r u = –30 cm
∴ Object should be placed at a distance at a of 30 cm on the left side of the concave lens.
Linear magnification, 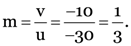
The positive sign of m shows that the image is virtual and erect, and its size of the object.
-
Here, focal length of concave lens, f1 = –25 cm
Focal length of convex lens, f2 = +20 cm
Power of the combination P = ?
Focal length of the combination F = ?
As 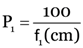
∴ 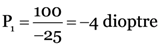
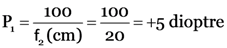
As P = P1 + P2
∴ P = –4 + 5 = 1 dioptre
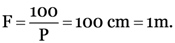
Positive sign with P and F indicates that the combination of two given lenses behaves as a convex lens.
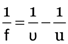
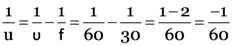
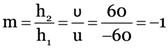

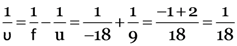
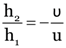
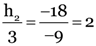
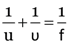
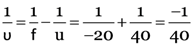
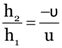
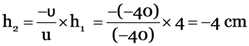
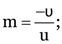
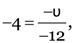 v = –48 cm.
v = –48 cm.