Electricity Worksheet-7

Electricity Worksheet-7

6. Calculate the equivalent resistance of the network across the points A and B shown in the figure.

7. Three resistors are connected as shown in the figure. Through the resistor of 5 Ω, a current of 1 A is flowing.

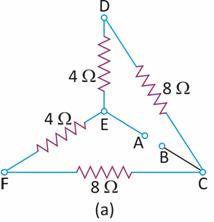
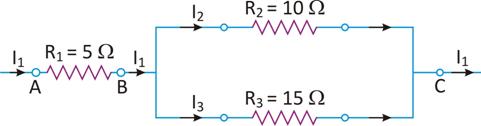
(a) Find the potential difference across AB and across AC?

(b) Find the current through the other two resistors?

(c) Find the total resistance?

8. A 24 volt battery is connected to the arrangement of resistances shown in fig.  calculate (i) the total effective resistance of the circuit, (ii) the total current flowing in the circuit.

9. Three resistors of 6 Ω, 3 Ω and 2 Ω are connected together so that the total resistance is greater than 6 Ω but less than 8 Ω. Draw a diagram to show this arrangement and calculate its total resistance.

10. For the combination of resistors shown in the figure, find the equivalent resistance between (i) C and D and (ii) A and B.

Answer:

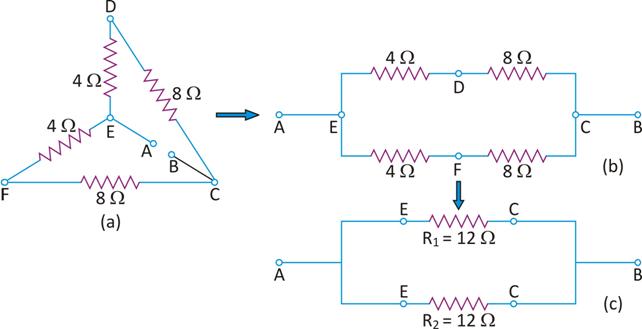
The given network, shown in the figure a, can be represented as shown in figure b.

The resultant of 4 Ω and 8 Ω resistances, which are in series in the arm EDC, is given by

          R₁ = 4 Ω + 8 Ω = 12 Ω

Similarly, the resultant of 4 Ω and 8 Ω in the arm EFC is given by

          R₂ = 4 Ω + 8 Ω = 12 Ω

The equivalent circuit of R₁ and R₂ which are in parallel is shown in figure c.                                                     

If R is the equivalent resistance between the point A and B, then

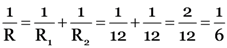
Or     R = 6 Ω

7. (a)    As current (I₂) through R₁ is 1 A,

          Potential difference across AB = V₁ = I₁R₁ = 1 × 5 = 5V

          Since R₂ and R₃ are in parallel, resultant resistance between B and C is given by

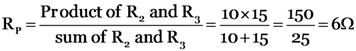
          Potential difference across BC, i.e.,

V₂ = I₁ R_P = 1 × 6 = 6V (∵ current through BC is I₁, i.e., 1 A)

          Potential difference  across AC

         = Potential difference across AB + Potential difference across BC = 5 V + 6 V = 11 V

(b) current through R₂, i.e.,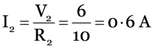

       (∵ Potential difference  across R₂ is the same as across BC)       

          Current through , i.e., I₃ = I₁ – I₂ = 1A – 0.6 = 0.4 A

 (c) Total resistance between A and C, i.e., R = R₁ + R_P = 5Ω + 6Ω = 11Ω

          The resultant of R₂ and R₃ which are in parallel is R_P; and R₁ and R_P are in series

8. R₁ is the equivalent resistance of 5Ω and 20Ω which are in series,

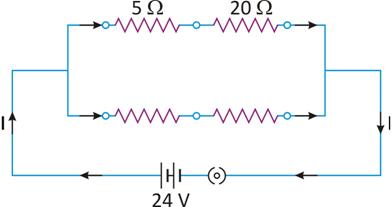
          R₁ = 5Ω + 20Ω = 25Ω

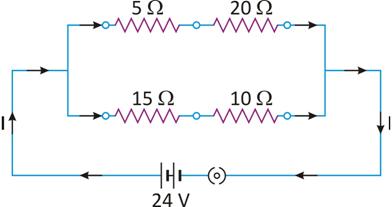
          R₂ is the equivalent resistance of 15Ω and 10Ω which are in series,

          R₂ = 15 Ω + 10 Ω = 25 Ω

          Now R₁ and R₂ are in parallel so final resistance is given by

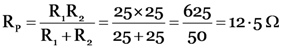
Total potential difference across the arrangement of all the resistances is 24 V

          Total current in the circuit,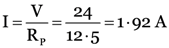

9. Here the total resistance has to be greater than 6Ω, therefore, 6Ω resistance should be in series with some other resistance. Now the total resistance is less than 8Ω, the other two resistances should be in parallel and their combination be connected in series with 6Ω resistance. Now R_P is the resultant of two resistances of 3Ω and 2Ω in parallel, then

          ,

i.e.,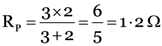  

Since R_P and 6Ω are in series, total resistance of the combination, i.e.,

          R = 6 + R_P = 6 + 1.2 = 7.2Ω

10. (i)     The resistors R₂, R₃ and R₄ are in series. Their equivalent resistance R_s is given by

          R_s = 3Ω + 3Ω + 3Ω  = 9Ω

          Further, R_s (= 9Ω) and R₅ (= 3Ω) are in parallel so their equivalent resistance is given by

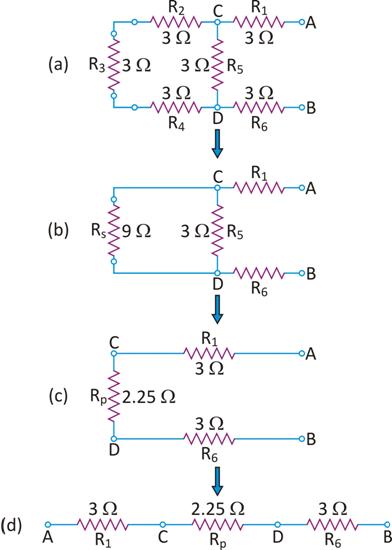
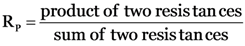
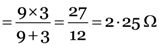
          Thus, the equivalent resistance between C and D is 2.25 Ω.

(ii)    Now R₁ (= 3Ω), R_P (= 2.25 Ω)

          and   R₆ (= 3 Ω)

          Are in series

Thus, equivalent resistance between A and B,

          = R₁ + R_P + R₆

          = 3 + R_P + R₆

          = 3 + 2.25 + 3

          = 8.25 Ω