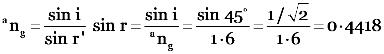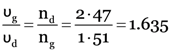Light reflection and refraction Worksheet-7
-
An object is placed at a large distance in front of a convex mirror of radius of curvature 40 cm. How far is the image behind the mirror ?
-
An object is placed 15 cm from a convex mirror of radius of curvature 90 cm. Calculate position of the image and its magnification.
-
The image formed by a convex mirror of focal length 30 cm is a quarter of the object. What is the distance of the object from the mirror ?
-
When an object is placed at a distance of 60 cm from a convex spherical mirror, the magnification produced is 1/2. Where should the object be placed to get a magnification of 1/3 ?
-
An object is placed 18 cm in front of a spherical mirror. If the image is formed at 4 cm to the right of the mirror, calculate its focal length. Is the mirror convex or concave ? What is the nature of the image ? What is the radius of curvature of the mirror ?
-
A convex mirror used for rear view on an automobile has a radius of curvature of 3.00 m. If a bus is located at 5.00 m from this mirror, find the position, nature and magnification of the image.
-
Calculate speed of light in water of refractive index 4/3. Given speed of light in air = 3 × 108 m/s.
-
A ray of light passes from air to glass (n = 1.5) at an angle of 30°. Calculate the anglt of refraction.
-
A ray of light is incident on a glass slab at an angle of 45°. If refractive index of glass be 1.6, what is the angle of refraction ?
-
The refractive index of diamond is 2.47 and that of glass is 1.51. How much faster does light travel in glass than in diamond?
Answer:
-
Here R = 40 cm, u = ∞, v = ?
As 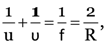
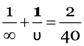
v = 20 cm.
-
Here u = –15 cm, R = 90 cm
v = ? m = ?
As 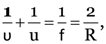
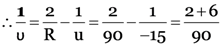
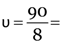 11.25
11.25
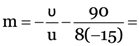 0.75.
0.75.
-
Here, f = 30 cm,
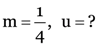
As 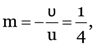
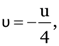
As 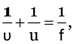
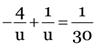 or
or 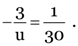
u = –90 cm.
-
Here, u = –60 cm,
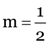
As 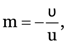
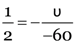
v = 30cm
As 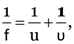
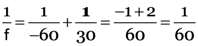
f = 60 cm
Again 
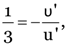
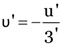
As 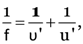
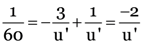
u’ = –120 cm.
-
Here, u = –18 cm, v = 4 cm, f = ?, R = ?
As 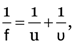
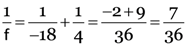
 5.14 cm
5.14 cm
As f is +, therefore, mirror is convex. Image is virtual, erect and smaller in size.
R = 2 f = 2 × 5.14 = 10.28 cm.
-
Here, R = 3.00 m, u = –5.00 m, v = ?, m = ?
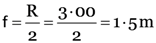
From 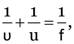
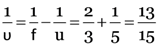
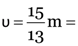 1.15 m
1.15 m
The image is virtual, erect and 1.15 m at the back of the mirror
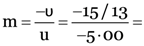 0.23.
0.23.
-
Here,
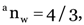
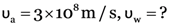
From 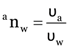
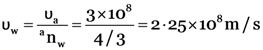 .
.
-
Here,
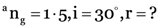
From 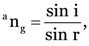
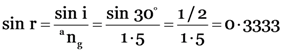
or r = 19.47°
-
Here, I = 45°,
 = 1.6; r = ?
= 1.6; r = ?
From 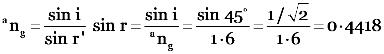
Using tables of natural sines, r = 26.2°
-
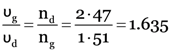
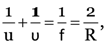
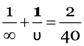
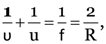
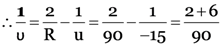
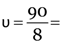 11.25
11.25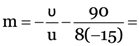 0.75.
0.75.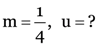
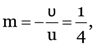
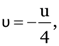
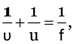
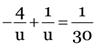 or
or 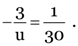
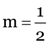
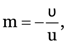
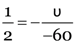
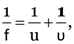
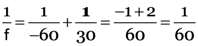

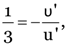
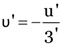
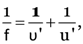
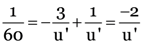
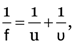
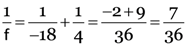
 5.14 cm
5.14 cm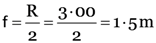
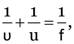
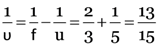
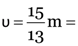 1.15 m
1.15 m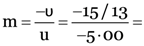 0.23.
0.23.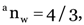
 .
.
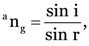
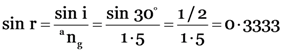
 = 1.6; r = ?
= 1.6; r = ?