Solution of a right angled triangle:
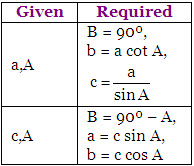
(i) When two sides are given: Let the triangle be right angled at C. Then we can determine the remaining elements as given in the following table.
.jpg)
(ii) When a side and an acute angle are given: In this case, we can determine the remaining elements as given in the following table
Solution of a triangle in general:
(i) When three sides a, b and c are given:
Δ = √s(s – a)(s – b)(s – c), where 2s = a + b + c = perimeter of triangle
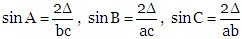
.jpg)
(ii) When two sides a, b and the included angle C are given:
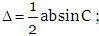
.jpg)
.jpg) and
and .jpg)
(iii) When one sides a and two angles A and B are given
A + B + C = 180º
⇒ C = 180º – A – B
b = ((a sin B)/(sin A)) and c = (a sin c)/(sin A) ⇒ Δ = (1/2) c a sin B
(iv) When two sides a, b and the angle A opposite to one side is given
sin B = (b/a) sin A .....(i)
c = 180º – (A + B), c = (a sin C)/(sin A)
Special Cases
Case I: When A is an acute angle:
(a) If a < b sin A, there is no triangle. When a < b sin A, then (i), sin B > 1, which is impossible.
.jpg)
(b) If a = b sin A, then only one triangle is possible which is right angled at B. When a = b sin A, then from sine rule. sin B = 1, ∴ ∠B = 90º from fig. It is clear that CB = a = b sin A
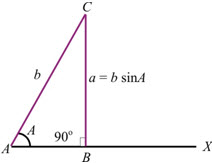
Thus, in this case, only one triangle is possible which is right angled at B.
(c) If a > b sin A, then three possibilities will arise:
(i) a = b In this case, from sine rule sin B = sin A
or B = 180º – A.
But B = 180º – A ⇒ A + B = 180º, which is not possible in a triangle. ∴ In this case, we get ∠A = ∠B.
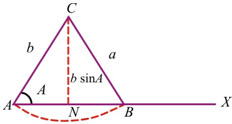
Hence, if b = a > b sin A then only one isosceles triangle ABC is possible in which ∠A = ∠B.
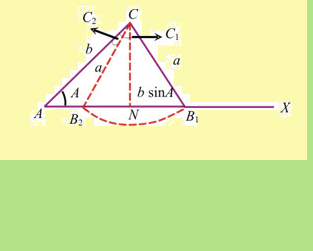
(ii) a > b In the following figure, Let AC = b, ∠CAX = A, and a > b, also a > b sin A.
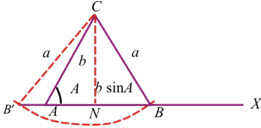
Now taking C as centre, if we draw an arc of radius a, it will intersect AX at one point B and hence only one ΔABC is constructed.
Also this arc will intersect XA produced at B' and ΔAB'C is also formed but this Δ is inadmissible (because ∠CAB' is an obtuse angle in this triangle)
Hence, if a > b and a > b sin A, then only one triangle is possible.
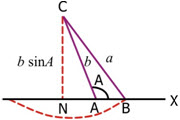
(iii) b > a (i.e., b > a > b sin A)
In fig. let AC = b, ∠CAX = A. Now taking C as centre, if we draw an arc of radius a, then it will intersect AX at two points B1 and B2. Hence if b > a > sin A, then there are two triangles.
.jpg)
Case II: When A is an obtuse angle:
► In this case, there is only one triangle, if a > b
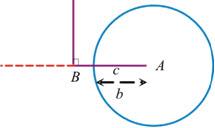
Case III: b > c and B = 90º:
► Again the circle with A as centre and b as radius will cut the line only in one point. So, only one triangle is possible.
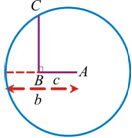
Case IV: b ≤ c and B = 90º
► The circle with A as centre and b as radius will not cut the line in any point. So, no triangle is possible.
► This is, sometimes called an ambiguous case.
Alternative Method:
► By applying cosine rule, we have cos B = (a2 + c2 – b2)/2ac
⇒ a2 – (2c cos B)a + (c2 – b2) = 0
⇒ a = cos B ± √(c cos B)2 – (c2 – b2)
⇒ a = c cos B ± √b2 – (c sin B)2
► This equation leads to following cases:
Case I:
► If b < sin B, no such triangle is possible.
Case II:
► Let b = c sin B, there are further following case.
(a) B is an obtuse angle
⇒ cos B is negative. There exists no such triangle.
(b) B is an acute angle
⇒ cos B is positive. There exists only one such triangle.
Case III:
► Let b > c sin B. There are further following cases :
(a) B is an acute angle ⇒ cos B is positive.
► In this case two values of a will exists if and only if c cos B > √b2 – (c sin B)2 or c > b. Two such triangle is possible. If c < b, only one such triangle is possible.
(b) B is an obtuse angle ⇒ cos B is negative. In this case triangle will exist if and only if √(b2 – (c sin B)2) > |c cos B| ⇒ b > c. So, in this case only one such triangle is possible. If b < c there exists no such triangle.