Force and laws of motion Worksheet-3

Force and laws of motion Worksheet-3

Which of the following effect cannot be produced by an unbalanced force acting on a body ?

A. Change in speed of the body.

B. Change in shape of the body

C. Change in direction of motion of the body

D. Change is state of rest of the body

What force would be needed to produce an acceleration of 4 m/s² in a ball of mass 6 kg ?

A. 24 newtons B. 24 kg

C. 12 newtons D. 1.5 newtons

What is the acceleration produced by a force of 12 newtons exerted on an object of mass 3 kg ?

A. 2 m/s² B. 36 m/s² C. 4 m/s² D. 4 m/s

Calculate the force required to impart to a car having velocity of 30 m/s in 10 seconds starting from rest. The mass of the car is 1500 kg.

A. 4500 kg B. 500 N C. 4000 N D. 4500 N

The speed-time graph of a car is given alongside. The car weighs 1000 kg.

What is the braking force applied at the end of 5 seconds to bring the car to a stop within one second ?

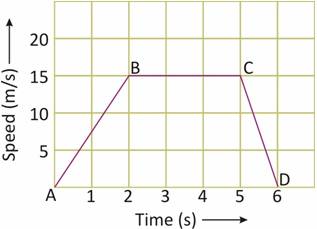
A. –15000 N B. 15000 N C. –5000 N D. 10000 N

The speed-time graph of a car is given alongside. The car weighs 1000 kg.

What is the distance travelled by the car in the first two seconds ?

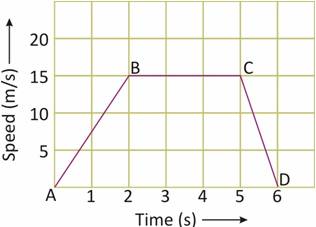
A. 90 m B. 7.5 m C. 30 m D. 15 m

A truck starts from rest and rolls down a hill with constant acceleration. It travels a distance of 400 m in 20 s. find its acceleration. Find the force acting on it if its mass is 7 metric tones.

A. 14000 N B. -14000 N

C. 14000 kg D. -14000 kg

A force of 5 newtons gives a mass m₁ an acceleration of 8 m/s², and a mass m₂ an acceleration of 24 m/s². What acceleration would it give both the masses are tied together ?

A. 6 m/s B. 32 m/s² C. 6 m/s² D. 16 m/s²

Which would require a greater force ?

(a) accelerating a 10 g mass at 5 m/s²

(b) a 20 g mass at 2 m/s²?

A. accelerating a 10 g mass at 5 m/s²

B. a 20 g mass at 2 m/s²?

C. Same force is required

D. Can’t say

A bullet of mass 10 g is fired from a gun of mass 6 kg with a velocity of 300 m/s. calculate the recoil velocity of the gun.

A. 0.5 m/s B. 50 m/s C. 0.5 m/s² D. 1 m/s

Answer:

Explanation: The force needed can be calculated by using the relation :

Force = mass × acceleration

Or F = m × a

Here, force, F = ?

Mass, m = 6 kg

Acceleration, a = 4 m/s²

Now, putting these values of m and a in the equation, we get :

F = 6 × 4

Force F = 24 N

Thus, the force needed is of 24 newtons.

Explanation: force F = 12 N

Mass m = 3 kg

acceleration a = ?

Now, F = m × a

So, 12 = 3 × a

3a = 12

a = (12/3) m/s²

Acceleration, a = 4 m/s²

Explanation: Mass m = 1500 kg

Using the first equation of motion.

Initial velocity, u = 0 (car starts from rest)

Final velocity, v = 30 m/s

Time taken t = 10 s

Now, putting these values in the equation :

v = u + at

30 = 0 + a × 10

10a = 30

a = (30/10) m/s²

acceleration, a = 3 m/s²

By putting m = 1500 kg and a = 3 m/s² in formula

F = m × a

F = 1500 × 3 N

= 4500 N

Thus the force required in this case is of 4500 newtons.

Explanation: First let’s calculate the distance travelled in the first two seconds.

From the given graph we find that :

Distance travelled in first two seconds = Area under line AB and the time axis

= Area of triangle AB2 = (1/2) × base × height = 15 m

Thus, the distance travelled by the car in the first two seconds is 15 metres.

The braking force is to be calculated by using the formula :

F = m × a

Here the mass of the car is given as 1000 kg. The acceleration in the last one second (from point C to point D) can be calculated from the graph. Now, the acceleration is given by the slope of speed-time graph.

Acceleration in last one second = slope of line CD

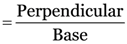
= 15 m/s²

If we observe the graph, we will find that the speed of the car is decreasing from point C to point D. That means the acceleration from C to D is negative so it should be written with a minus sign.

Acceleration, a = –15 m/s²

Force F = 1000 × (–15)

= -15000 N

The negative sign of force here shows that the force is being applied in a direction opposite to the motion of the car. That is, it is a retarding force.

Explanation: First let’s calculate the distance travelled in the first two seconds.

From the given graph we see that :

Distance travelled by car in first two seconds = Area under line AB and the time axis

= Area of triangle AB2

= (1/2) × base × height (Altitude)

= (1/2) × 2 × 15

= 15 m

Thus, the distance travelled by the car in the first two seconds is 15 metres.

Explanation: Let’s find its acceleration by using equation of motion :

Distance travelled s = ut + (1/2)at²

s = 400 m

Initial speed, u = 0 (As it starts from rest)

Time, t = 20 s

acceleration a = ?

By Putting these values in the above formula :

400 = 0 × 20 + (1/2) × a × (20)²

400 = 200 a

a = 2 m/s² …….(1)

Let’s now calculate the force by using the relation :

F = m × a

Mass, m = 7 metric tones

= 7 × 1000 kg

= 7000 kg …….(2)

acceleration, a = 2 m/s²

Force, F = 7000 × 2

F = 14000 N

Thus the force acting on the truck is 14000 newtons.

Explanation:

(i) First case :

Force F = 5 N

Mass, m = m₁

acceleration, a = 8 m/s²

Now, F = m × a

5 = m₁ × 8

m₁ = 0.625 kg

Hence mass m₁ is 0.625 kg.

(ii) Second case :

Force, F = 5 N

Mass, m = m₂

acceleration, a = 24 m/s²

5 = m₂ × 24

m₂ = 5/24 kg

Thus, the mass, m₂ is 5/24 kg.

(iii) Third case :

Force F = 5 N

Total mass m = m₁ + m₂

= 0.625 + 5/24

= 0.833 kg

acceleration, a = ?

By putting these values in the relation :

F = m × a

5 = 0.833 × a

a = 6 m/s²

Thus, if both the masses are tied together, then the acceleration would be 6 m/s².

Explanation:

(i) In the first case :

Force, F = m × a

= (10/1000) kg × 5 m/s²

= 0.05 N …….(1)

(ii) In the second case :

Force, F = (20/1000) kg × 2 m/s²

= 0.04 N ……..(2)

Thus, a greater force of 0.05 N is required for accelerating a 10 g mass.

Explanation: Given mass of bullet = 10 g = (10/1000) = 0.01 kg

Velocity of bullet = 300 m/s

Mass of gun = 6 kg

Recoil velocity of gun = ?

Now, putting these values in the relation:

Mass of Bullet × velocity of Bullet = Mass of gun× Recoil velocity of gun

0.01 × 300 = 6 × Recoil velocity of gun

Recoil velocity of gun = (0.01 × 300)/6

= 0.5 m/s