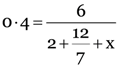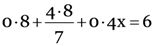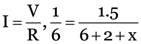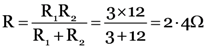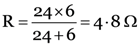Electricity Worksheet-8
-
An electric lamp, whose resistance is 20 Ω and a conductor of 4 Ω resistances are connected to a 6 V battery as shown in the figure. Calculate the total resistance of the circuit, the current through the circuit and the potential difference across the electric lamp and the conductor.
-
Three resistors of 2Ω, 3Ω and 4Ω are connected in (a) series (b) parallel. Find the equivalent resistance in each case.
-
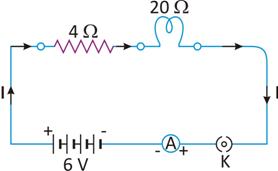
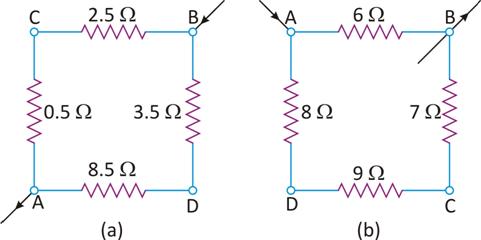
Calculate the equivalent resistance between the points A and B in the circuits shown in figures.
-
A combination consists of three resistors in series. Four similar sets are connected in parallel. If the resistance of each resistor is 2 Ω, find the resistance of this combination.
-
A circuit consists of 1 Ω wire in series with a parallel arrangement of 6 Ω and 3 Ω wires. Calculate the total resistance of the circuit.
-
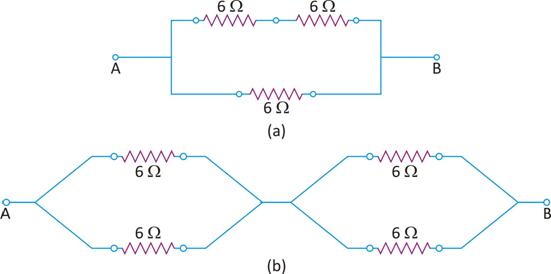
Calculate the effective resistances between the point A and B in the networks shown here.
-
Two resistors 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. Calculate (i) the current through the battery (ii) current through each resistor.
-
Carefully study the circuit diagram and calculate the value of x.
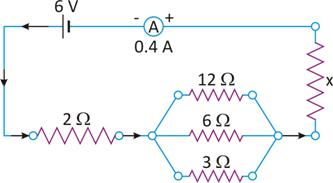
-
Three resistors of 6 Ω, 2 Ω and x are connected in series to a cell of emf 1.5V. the current registered is (1/6)A. calculate the value of x.
-
Calculate the equivalent resistances between the point A and B of the circuits shown here
Answer:
-
Since the lamp and conductor are in series,
total resistance in the circuit, Rs = 20 Ω + 4 Ω = 24 Ω
current through the circuit, 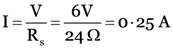
Potential difference across the lamp, V1 = IR1 = 0.25 A × 20 Ω = 5V
Potential difference across the conductor, V2 = IR2 = 0.25 A × 4Ω = 1V
-
(a) Rs = 2 Ω + 3 Ω + 4 Ω = 9 Ω
(b) 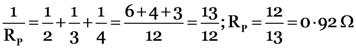
-
(a) Two resistances (6 Ω, 6 Ω) are in series and their resultant resistance = 6 Ω + 6 Ω = 12 Ω. Further, 12 Ω and 6 Ω are in parallel. The resultant resistance of 12 Ω and 6 Ω in parallel is
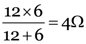 .
.
(b) The resultant resistance of 6 Ω, 6 Ω which are in parallel in the first loop is 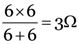 and resultant resistance in the second loop is also 3 Ω. Since the two loops are in series, the total resistance between A and B is 3 Ω + 3 Ω = 6 Ω.
and resultant resistance in the second loop is also 3 Ω. Since the two loops are in series, the total resistance between A and B is 3 Ω + 3 Ω = 6 Ω.
-
Resistance of a combination of 3 resistors (each of resistance 2 Ω) in series = 6 Ω
Resistance of 4 sets of such combinations in parallel 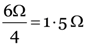 .
.
-
Resistance of parallel combination of 6 Ω and 3Ω
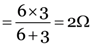
Since 2 Ω and 1 Ω are in series, resultant resistance = 2 Ω + 1 Ω = 3 Ω.
-
1 Ω and 2 Ω are in series and their resultant resistance is
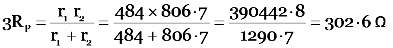 . Now 3 Ω and 1.5 Ω are in parallel and their equivalent resistance
. Now 3 Ω and 1.5 Ω are in parallel and their equivalent resistance 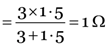
Resistance in the arm ACB, i.e., R1 = 5Ω; resistance in the arm ADB, i.e., R2 = 5Ω. Now, R1, 1Ω and R2 are in parallel.
If R is their equivalent resistance, 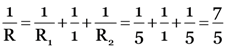 or
or 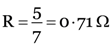
-
If R is the resultant resistance of 4 Ω and 6 Ω in parallel, then
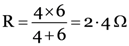 .
.
Current through the battery, 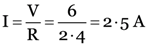
Since the resistors are in parallel, the potential difference
across each is the same, i.e., V.
Current through 4 Ω resistor 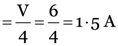
and current through 6 Ω resistance 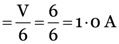
-
The resistances 12 Ω, 6 Ω and 3 Ω are in parallel. If R1 is their resultant resistance, then
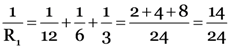 or
or 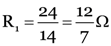
Since 2 Ω, R1 and x are in series,
Total resistance in the circuit, R = 2 + R1 + x = 2 + 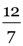 + x
+ x
From ohm’s law, 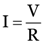 or
or 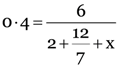
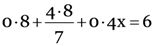
0.4x = 4.514
x = 11.3 Ω
-
As
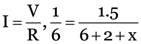
Or 8 + x = 9 or x = 1 Ω
-
(a) total resistance in the path ACB, i.e., R1 = 0.5 Ω + 2.5 Ω = 3 Ω
Total resistance in the path ADB, i.e.,
R2 = 8.5 Ω + 3.5 Ω = 12 Ω
Since R1 and R2 are in parallel, the effective resistance between the points A and B, i.e.,
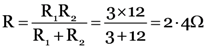
(b) total resistance in the path ADCB, i.e., R1 = 8 + 9 + 7 = 24 Ω
Further, R1 (= 24 Ω) and 6 Ω are in parallel between the points A and B.
Thus, effective resistance between A and B, i.e., 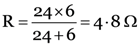





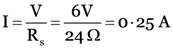
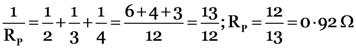
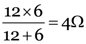 .
.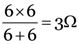 and resultant resistance in the second loop is also 3 Ω. Since the two loops are in series, the total resistance between A and B is 3 Ω + 3 Ω = 6 Ω.
and resultant resistance in the second loop is also 3 Ω. Since the two loops are in series, the total resistance between A and B is 3 Ω + 3 Ω = 6 Ω.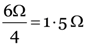 .
.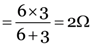
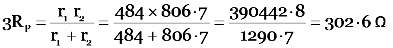 . Now 3 Ω and 1.5 Ω are in parallel and their equivalent resistance
. Now 3 Ω and 1.5 Ω are in parallel and their equivalent resistance 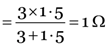
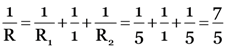 or
or 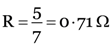
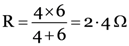 .
.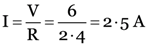
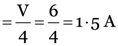
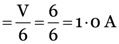
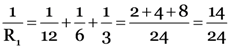 or
or 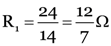
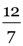 + x
+ x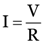 or
or