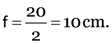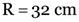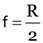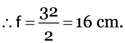Light reflection and refraction Worksheet-9
-
An object is placed at a distance or 50 cm from a concave lens of focal length 30 cm. Find the nature and position of the image.
-
An object of height 2 cm is placed at a distance of 15 cm in front of a concave lens of power –10 dioptre. Find the size of the image.
-
A thin lens has a focal length of –25 cm. What is the power of the lens ? Is it convex or concave ?
-
The power of lens is 2-5 D. What is its focal length?
-
A convergent lens of power 8 D is combined with a divergent lens of power –10 D. Calculate focal length of the combination.
-
A concave lens is kept in contact with a convex lens of focal length 20 cm. The combination works as a converging lens of focal length 100 cm. Calculate power of concave lens.
-
Find the focal length and nature of lens which should be placed contact with a lens of focal length 10 cm so that the power of the combination becomes 5 dioptre.
-
The radius of curvature of a spherical mirror is 20 cm. What is its focal length ?
-
Name a mirror that can give an erect and enlarged image of an object.
-
Find the focal length of a convex mirror whose radius of curvature is 32 cm.
Answer:
-
Here, = –50 cm, f = –30 cm, v = ?
As 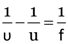
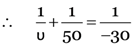
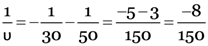
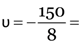 –18.7 cm
–18.7 cm
As v is negative, the image must be virtual and erect.
-
Here, h1 = 2cm, u = –15 cm
P = –10D, h2 = ?
Now, 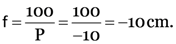
As 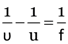
∴ 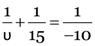
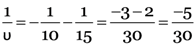
 As v is negative, image is virtual
As v is negative, image is virtual
As 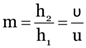
∴ 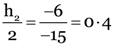
h2 = 0.8 cm. As h2 is positive, image is erect.
-
Here,
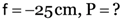
From 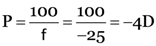
Negative sign shows that lens is concave.
-
Here,
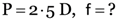
∴ 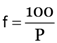
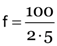 = 40 cm.
= 40 cm.
-
Here, P1 = 8 D, P2 = –10 D, f = ?
As P = P1 + P2 = 8 – 10 = –2D
∴  –0.5 m
–0.5 m
-
Here, f1 = 20 cm,
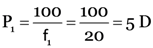
F = 100 cm, 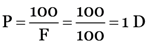
As P1 + P2 = P, ∴ P2 = P – P1 = 1 – 5 = –4 D
-
Here, f1 = ?, f2 = 10 cm,
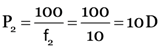
P = 5D.
As P1 + P2 = P
∴ P1 + 10 = 5 or P1 = 5 – 10 = – 5D.
∴ 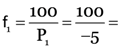 –20 cm.
–20 cm.
Lens must be concave.
-
Here, R = 20 cm, f = ?
As 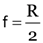 ∴
∴ 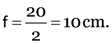
-
A concave mirror gives an erect and enlarged image of an object held between pole and principal focus of the mirror.
-
Here, focal length, f = ?
radius of curvature, 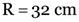
As 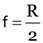
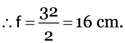
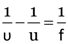
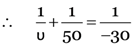
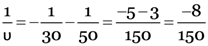
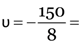 –18.7 cm
–18.7 cm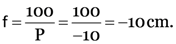
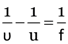
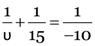
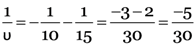
 As v is negative, image is virtual
As v is negative, image is virtual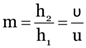
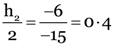
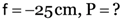
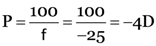
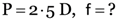
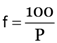
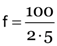 = 40 cm.
= 40 cm. –0.5 m
–0.5 m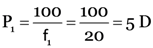
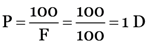
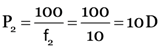
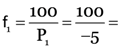 –20 cm.
–20 cm.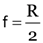 ∴
∴