Work and Energy Worksheet-2
A. 10 joules B. 1 joule C. 0 joule D. None of these
A. 1200 J B. 12000 J C. 120 J D. 0 J
A. 12.5 J B. 0 J C. 50 J D. 25 J
A. 0.01 J B. 0.02 J C. 0.04 J D. None of these
A. 3 : 1 B. 9 : 1 C. 1 : 3 D. 1: 9.
A. 210 J B. 40 J C. 250 J D. 290 J
A. 250 J B. 50 J C. 100 J D. None of these
A. 5 m B. 10 m C. 2.5 m D. 20 m
A. 4 W B. 80 W C. 0.2 W D. None of these
A. 20 KW B. 200 KW C. 2000 KW D. 2 kW
Answer:
Explanation: The work done is calculated by using the formula :
W = F × S
Force, F = 10 N
Distance, S = 1 m
Work done W = 10 × 1 J = 10 J
Thus, the work done is 10 joules.
Explanation: In this case work is being done against gravity in lifting water. Now the formula the work done against gravity is :
W = m × g × h
Mass of water, m = 200 kg
Acceleration due to gravity g = 10 m/s2
Height h = 6 m
By putting the values in the we get :
W = 200 × 10 × 6
W= 12000 J
Thus, the work done is 12000 joules.
Explanation:
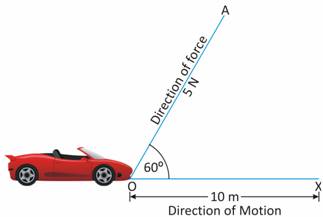
The toy car is moving along horizontal floor, so we can draw a horizontal line OX to show the direction of motion the car. Now the force of 5 N is applied along the string tied to the toy car making an angle of 60° with the floor. Now we draw another line OA making an angle of 60° with horizontal floor OX. In the diagram, OX represents the direction of motion and OA represents the direction of force, the angle between them being 60°.
Now the formula for work done when a body moves at an angle to the direction of force is :
W = F cos θ × S
Here, Force, F = 5 N
Angle θ = 60°
Distance, s = 10 m
So, Work done, W = 5 × cos 60° × 10
cos 60° = 0.5.
W = 5 × 0.5 × 10 = 25 J
Thus, the work done is 25 joules.
Explanation: Kinetic energy = (1/2) mv2
Mass, m = 2 kg
Velocity, v = 0.1 m/s
Kinetic energy = (1/2) × 2 × (0.1)2
= (1/2) × 2 × 0.1 × 0.1
= 0.01 J
Thus, the kinetic energy of the body is 0.01 joule.
Explanation:
(i) Mass of first body = m
Velocity of first body = v
So, K.E. of first body = (1/2) mv2 ... (1)
(ii) Mass of second body = m
Velocity of second body = 3v
So, K.E. of second body = (1/2) m (3v)2
= 9/2 mv2 ...(2)
Now, to find out the ratio of kinetic energies of the two bodies, we should divide equation (1) by equation (2), so that:
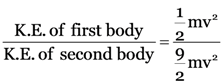
or 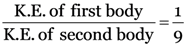
Thus, the ratio of the kinetic energies is 1: 9.
K.E. of second body = 9 × K.E. of first body
That is, the kinetic energy of second body is 9 times the kinetic energy of the first body.
Explanation: We know that whenever work is done, an equal amount of energy is used up.
Hence the work done in this case will be equal to the change in kinetic energy of bicycle when its speed changes from 2 ms–1 to 5 ms–1.
Initially
Mass of bicycle m = 20 kg
Speed of bicycle v = 2 ms–1
Kinetic energy, EK = (1/2) mV2
= 10 × 4
= 40 J
(b) In the second case :
Mass of bicycle, m = 20 kg
Speed of bicycle, v = 5 ms–1
So, Kinetic energy, EK = (1/2) mV2
= (1/2) × 20 × (5)2
= 10 × 25
= 250 J
Now, Work done = Change in kinetic energy
= 250 – 40
= 210 J
Thus, the work done is 210 joules.
Explanation:
The potential energy of a body is calculated by using the formula :
Potential energy = m × g × h
Mass, m = 1 kg
Acceleration due to gravity, g = 10 m/s2
Height, h = 5m
Potential energy = 1 × 10 × 5 = 50 J
Thus, the potential energy of the body is 50 joules.
Explanation:
Here, Potential energy, P.E. = 9800 J
Mass m = 200 kg
Acceleration due to gravity, g= 9.8 ms–2
Height, h= ?
P.E. = m × g × h
9800 = 200 × 9.8 × h
So, 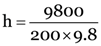
h = 5 m
Thus, the bag of wheat should be raised to a height of 5 meters.
Explanation:
Powers 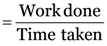
Work done = 20 J
Time taken = 5 s
Power = (20 J/ 5S) = 4 J/s
Thus, Power = 4 W (because 1 J/s = 1 W)
Thus, the power of this body is 4 watts.
Explanation: Let’s calculate the work done by the pump in lifting the water against the force of gravity.
W = m × g × h
Mass of water, m = 100 kg
Acceleration due to gravity, g = 10 ms–2
Height, h = 20 m
Work done, W = 100 × 10 × 20 = 20000 J
Time taken, t = 10 s
Now, we know that:
Power, P = (W/t)
= (20000/10) = 2000 watts (or 2000 W)
Thus, the power of this pump is 2000 watts. This power can be converted from watts into kilowatts by dividing it by 1000.
So, Power = (2000/1000) kilowatts
= 2 kilowatts (or 2 kW)