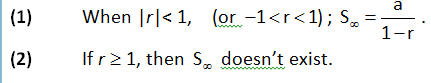Sequence and series-2

Properties of an A.P. 

If  a, b, c, d,...... are in A.P. whose common difference is d, then for fixed non–zero number k ∈ R.

1. a ± k, b ± k, c ± k..... will be in A.P., whose common difference will be d.
2. ka, kab, kac..... will be in A.P. with common difference = kd.
3. a/k, b/k, c/k..... will be in A.P. with common difference = d/k.

Means if an Arithmetic progression is multiplied or divided by a constant it still remains an Arithmetic progression. But the common difference is changed, it is multiplied or divided by the constant respectively.

The sum of terms of an A.P. equidistant from the beginning and the end is constant and is equal to sum of first and last term. i.e. a₁ + a_n = a₂ + a_n–1 = a₃ + a_n–2....

If number of terms of any A.P. is odd, then sum of the terms is equal to product of middle term and number of terms.

If number of terms of any A.P. is even then A.M. of middle two terms is A.M. of first and last term.

If the number of terms of an A.P. is odd then its middle term is A.M. of first and last term. 

If a₁, a₂, a₃, a₄.....an and b₁, b₂, b3, b₄.....b_n are two APs with common difference d₁ and d₂ respectively then

a₁ ± b₁, a₂ ± b₂, a₃ ± b₃...... are also in AP.

If a, b, c are in AP then 2b = a + c

If the terms of an A.P. are chosen at regular intervals, then they form an A.P.

Geometric Progression :

A progression is called a G.P. if the ratio of its each term to its previous term is always constant. This constant ratio is called its common ratio and it is generally denoted by r.

For example :

The sequence 4, 12, 36, 108, ….. is a G.P., because; 12/4 = 36/12= 108/38...... = 3 ( known as common ratio)

a, ar, ar², ar³, ar⁴......ar^n–1 are terms in GP and ar^n–1 is known as nth term of GP.

So If the first term is ‘a’ and the common ratio is ‘r’.

The general term or n^th term of a G.P. is = t_n = ar^n–1

p^th term from the end of a finite G.P.:

If G.P. consists of ‘n’ terms, p^th term from the end (n–p+1)^th term from the beginning = a r^n–p.

Selection of terms in a G.P. :

When the product is given, the following way is adopted in selecting certain number of terms:

3 terms = a/r, a, ar

4 terms = a/r³, a/r, ar, ar³

5 terms = a/r², a/r, a, ar, ar², 

When the product is not given, then the following way is adopted in selection of terms : 

a, ar, ar², ar³, ar⁴.....ar^n–1

Sum of first ‘n’ terms of a G.P. :

If a be the first term, r the common ratio, then sum S_n of first n terms of a G.P. is given by ;

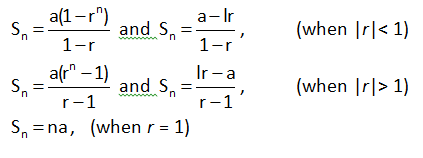
Sum of infinite terms of a G.P. :