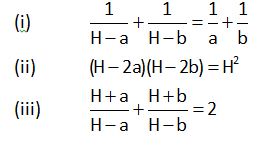Harmonic Progression (H.P.)
Definition:
A progression is called a harmonic progression (H.P.) if the reciprocals of its terms are in A.P.
Standard form: 1/a, 1/(a + d), 1/(a + 2d)......1, 1/2, 1/3,....... are in harmonic progression and 1, 2, 3..... are in arithmetic progression.
General term of an H.P.

Harmonic Mean:
If three or more numbers are in H.P., then the numbers lying between the first and last are called harmonic means (H.M.’s) between them. For example 1, 1/3, 1/5, 1/7, 1/9 are in H.P. So 1/3, 1/5 and 1/7 are three H.M.’s between 1 and 1/9.
Also, if a, H, b are in H.P., then H is called harmonic mean between a and b.
Insertion of Harmonic Means:
Single H.M. between a and b = 2ab/(a + b)
H, H.M. of n non-zero numbers a1, a2, a3, a4,.....an is given by ;
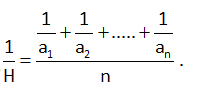
Let a, b be two given numbers. If n numbers H1, H2, H3.....Hn are inserted between a and b such that the sequence a H1, H2, H3.....Hn b is a H.P., then H1, H2, H3.....Hn are called n harmonic means between a and b.
Now, a H1, H2, H3.....Hn b are in H.P.
1/a, 1/H1, 1.H2, 1/H3.....1/Hn, 1/b are in AP.
Let D be the common difference of this A.P. Then,
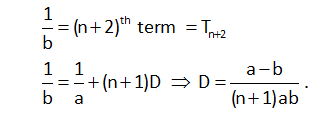
Thus, if n harmonic means are inserted between two given numbers a and b, then the common
difference of the corresponding A.P. is given by
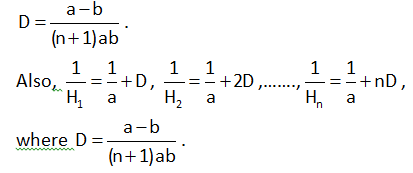
Properties of H.P. :
No terms of HP can be zero
If H is the H.M. between a and b, then