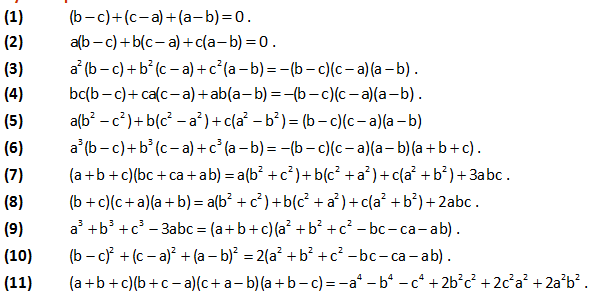Methods of Finding Factors:
Taking Out Common Factors: Place the common factor outside as a coefficient and divide each term separately by same factor.
Factors by Grouping the Terms: An expression having even number of terms may be resolved into factors if the terms are arranged in groups such that each group has a common factor.
Factorizing the Trinomials of The form ax2 + bx + c:
If the product ‘ac’ is positive, find two numbers whose sum is ‘b’ and product is ‘ac’. If the product ‘ac’ is negative, find two numbers whose difference is ‘b’ and product is ‘ac’. Then rewrite equation replacing b by sum (difference) of a and c.
Factorization of the Sum of or Difference of Two Cubes:
If we divide a3 + b3 by (a + b), the quotient is a2 – ab + b2 and if we divide a3 – b3 by (a – b)¸ the quotient is a2 + ab + b2.
Some Important Formulae:
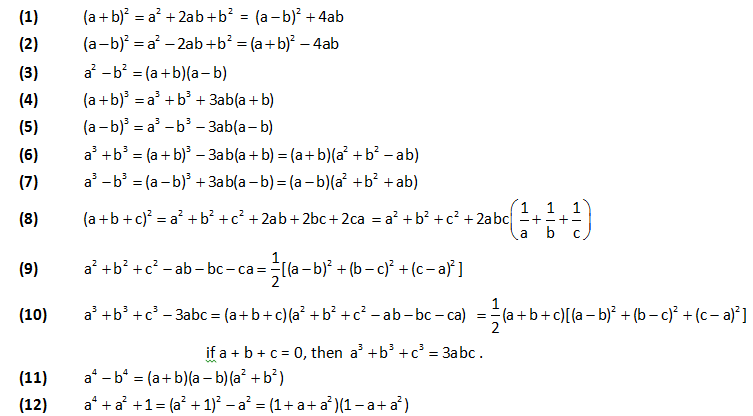
(a – b) is always a factor of (an – bn) where n is any positive integer.
(a + b) is always a factor of (an + bn) where n is any positive odd integer.
Important Identities
Cyclic Expressions: