Angle & Trigonometric Ratio

(a) Sexagesimal  (or English) System:

(b) Centesimal (OR French System):

(c) Circular System:

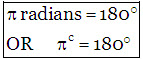
► Relation between three systems of measurement of angle

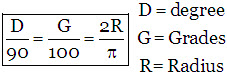
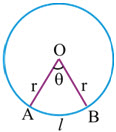
Area of a Sector of a Circle:

► Let AOB be a sector of a circle, centre O, radius r. Let ∠APB = θ radian arc AB = l. Then Area of the sector AOB = (1/2)r² θ.

Trigonometric Function:

(1) Fundamental Identities

sin² θ + cos² θ = 1

1 + tan² θ = sec² θ

1 + cos² θ = cosec²

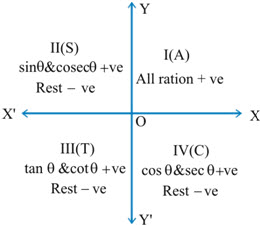
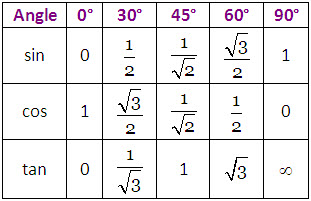
(2) Signs of Trigonometric ration is quadrants

► Angle θ & (90◦ – θ◦) are complementary angles, θ &  (180◦ – θ◦) are supplementary angles.

cos n π = (–1)ⁿ, n ∊ l

sin π  = 0, n ∊ l

cos (nπ/2) = 0 if n is odd integer

cos(nπ + θ) = (–1)ⁿ cos θ, if n ∊ l

cos(nπ + θ) = (–1)ⁿ sin θ, if n ∊ l

cos(2nπ ± θ) = cos θ, n ∊ l

tan(nπ ± θ) = tan θ, n 0 ∊ l

Trigonometric Ratio of Compound Angles:

(1)   sin(A ± B) = sin A cos B ± cos A sin B

cos(A ± B) = cos A cos ∓ sin A sin B

tan (A ± B) = (tan A ± tan B)/(1 ∓ tan A tan B)

(2)    sin 2A = 2 sin A cos A  = (2 tan A)/(1 + tan² A)

cos 2A = cos² A – sin² A = 2 cos² A – 1 = 1 – 2 sin² A = ((1 – tan² A) / (1 + tan² A)) tan 2A = (2 tan A)/(1 – tan² A)

(3)   

Sum and Difference Formulae:

(1)

(2)

(3) sin(A + B) sin (A – B) = sin² A – sin² B = cos² B – cos² A

(4) cos(A + B) cos(A – B) = cos² A – sin² B

(5) sin 3θ = 3 sin θ – 4 sin³ θ

(6) cos 3θ = 4 cos³ θ – 3 cos θ

(7)

(8)

(9)

(10)

Product into Sum or Difference:

► 2 sin A cos B = sin (A + B) + sin (A – B)

► 2 cos A sin B = sin (A + B) – sin (A – B)

► 2 cos A cos B = cos (A + B) + cos (A – B)

► 2 sin A sin B = cos (A – B) – cos (A + B)

T-Ratios of the Sum of Three or more Angles:

► sin (A + B + C) = sin A cos B cos C + cos A sin B cos C + cos A cos B sin C – sin A sin B sin C   

OR

sin (A + B + C) = cos A cos B cos C (tan A + tan B + tan C – tan A tan B tan C)

► cos (A + B + C) = cos A cos B cos C – sin A sin B cos C – sin A cos B sin C – cos A sin B sin C  

OR

cos (A + B + C) = cos A cos B cos C (1 – tan A tan B – tan B tan C – tan C tan A)

►

► If A + B + C = π, then

(a) sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C

(b) sin A + sin B + sin C =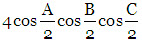

(c) cos 2A + cos 2B + cos 2C = –1 – 4 cos A cos B cos C

(d) cos A + cos B + cos C =

(e)

(f) tan A + tan B + tan C = tan A tan B tan C

(g)

(h) cot A cot B + cot B cot C + cot C cot A = 1

(i) tan A tan B + tan B tan C + tan C tan A = 1 + sec A sec B sec C

► The solution consisting of all possible solutions of a trigonometric equation is called its general solution.

sin θ = 0 ⇒ θ = nπ

cos θ  = 0 ⇒ θ = (2n + 1)(π/2)

tan θ = 0 ⇒ θ = nπ

sin θ = sin α ⇒ θ = nπ + (–1)ⁿ, α, α ∊ [(–(π/2)), (π/2)]

cos θ = cos α ⇒ θ = 2nπ ± α; α ∊ [0, π]

tan θ = tan α ⇒ θ = nπ + α; α ∊ [(–(π/2)), (π/2)]

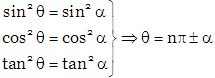
Principal Value:

Numerically least value of the angle is called its principal value.