Natural Numbers:
Counting numbers are known as natural numbers. 1, 2, 3, 4, 5,…., etc., are all natural numbers.
Whole Numbers:
All natural numbers together with 0 form the set of all whole numbers. Clearly, every natural number is a whole number. And, 0 is the only whole number that is not a natural number.
Integers:
All natural numbers, 0 and negatives of natural numbers form the set of all integers.
so, …., –4, –3, –2, –1, 0, 1, 2, 3, 4, …. etc., are all integers.
i. Even Integers:
Integers which are divisible by 2 are called even integers.
e.g., 0, ± 2, ± 4, …..
ii. Odd Integers:
Integers, which are not divisible by 2 are called as odd integers. e.g., ±1, ±3, ±5, ±7 ….
Prime Number:
Let ‘p’ be a natural number ‘p’ is said to be prime if it has exactly two distinct factors, namely 1 and itself.
e.g., 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …..
Composite Number:
Let ‘a’ be a natural number, ‘a’ is said to be composite if, it has atleast three distinct factors.
Note:
‘1’ is neither prime nor composite.
‘2’ is the only even prime number.
Number which are not prime are composite numbers (except 1).
‘4’ is the smallest composite number.
Co-Prime Numbers:
Two natural numbers (not necessarily prime) are co-prime, if there H.C.F. (Highest Common Factor) is one.
e.g., (1, 2), (1, 3), (3, 4), (3, 10), (3, 8), (5, 6), (7, 8) etc.
These numbers are also called as relatively prime numbers.
Note:
(a) Two distinct prime numbers are always co-prime but converse need not be true.
(b) Consecutive numbers are always co-prime numbers.
Twin Prime Numbers:
If the difference between two prime numbers is two, then the numbers are called as twin prime numbers. e.g., {3, 5}, {5, 7}, {11, 13}, {17, 19}, {29, 31}.
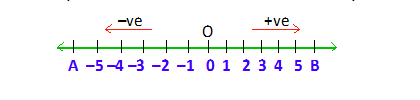
Number Line:
Draw a line AB which extends endlessly in both the directions as indicated by the arrowheads in the diagram below.
Rational Numbers:
A number which can be expressed in the form of p/q, where p and q are integers and q ≠ 0 is called a rational number.
4 is a rational number, since 4 = 8/2 , where 8, 2 are integers and 2 ≠ 0.
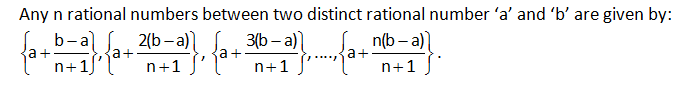
Irrational Numbers:
A number which is not a rational number is called an irrational number.
Thus, non-terminating and non-repeating decimals are irrational numbers.
For example,
(i) 0.01001000100001…
(ii) 0.343343333433334…
√2 = 1.4142313......
are non-terminating and non-repeating decimal numbers. So, these are example of irrational numbers.
A number √a (square root of a) is an irrational number if ‘a’ is positive and ‘a’ is not the square of a rational number.
For example,√2, √3, √5, √5/7 are all positive irrational numbers.
Similarly, -√3, -√5/7 , etc., are also irrational numbers which are negative irrational numbers.
A number n√a (nth root ‘a’) is also an irrational number if ‘a’ is positive and not a perfect nth power of a rational number.
It should be kept in mind that ∏ is an irrational number and 22/7 is a rational number because we take an approximate value of π as 22/7
Properties of Irrational Numbers:
If ‘a’ is irrational, ‘–a’ is also irrational.
The sum of a rational number and an irrational number is always irrational.
The product of a rational number (≠ 0) and an irrational number is always irrational.
The sum of two irrational numbers is not always an irrational number.
The product of two irrational numbers is not always an irrational number.
If ‘a’ and ‘b’ are rational and ‘ab’ is not a perfect square, √ab lies between ‘a’ and ‘b’ and is rational.
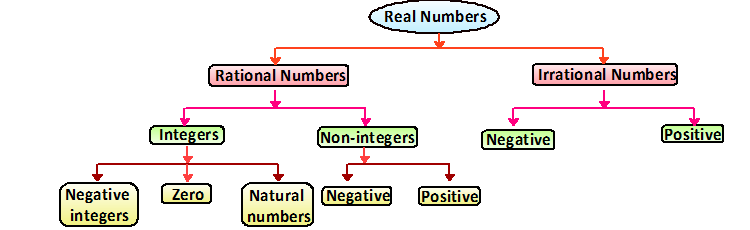
Real Numbers:
The collection of all rational and irrational numbers denoted by R is called the set of real numbers.
The notation x ÎR means, x is a real number.
Complex Number:
A number of the form a + ib is called complex number, where a, b ∈ R and √-1 . Complex number is usually denoted by C.
Note: If may be noted that N ⊂ W ⊂ I ⊂ R ⊂ C
Check some interesting questions :
The smallest prime number is :
How many prime nos are there from 1 to 100 ?
Which is the smallest composite number ?
Give an example of even prime number.
How many even prime numbers are there?
How many one digit prime numbers are there ?
What is the addition of first four prime numbers ?
Which is the smallest two digit composite number ?
Which is the smallest two digit prime number ?
Which is the biggest two digit prime number ?
Write 5 examples of coprime numbers.
Write 5 examples of twin prime numbers.